[99클럽/코딩테스트 챌린지/C++] 특정 거리의 도시 찾기 문제 해결 - BFS를 통한 최단 거리 탐색

오늘은 특정 거리의 도시 찾기 문제를 해결하면서 BFS(너비 우선 탐색)를 이용하여 최단 거리를 계산하는 방법을 복습했습니다. 이 문제는 특정 시작 도시에서 다른 도시들까지의 최단 거리를 탐색하고, 최단 거리가 정확히 K인 도시들을 찾는 것이 목표입니다.

문제 링크 : 

https://www.acmicpc.net/problem/18352

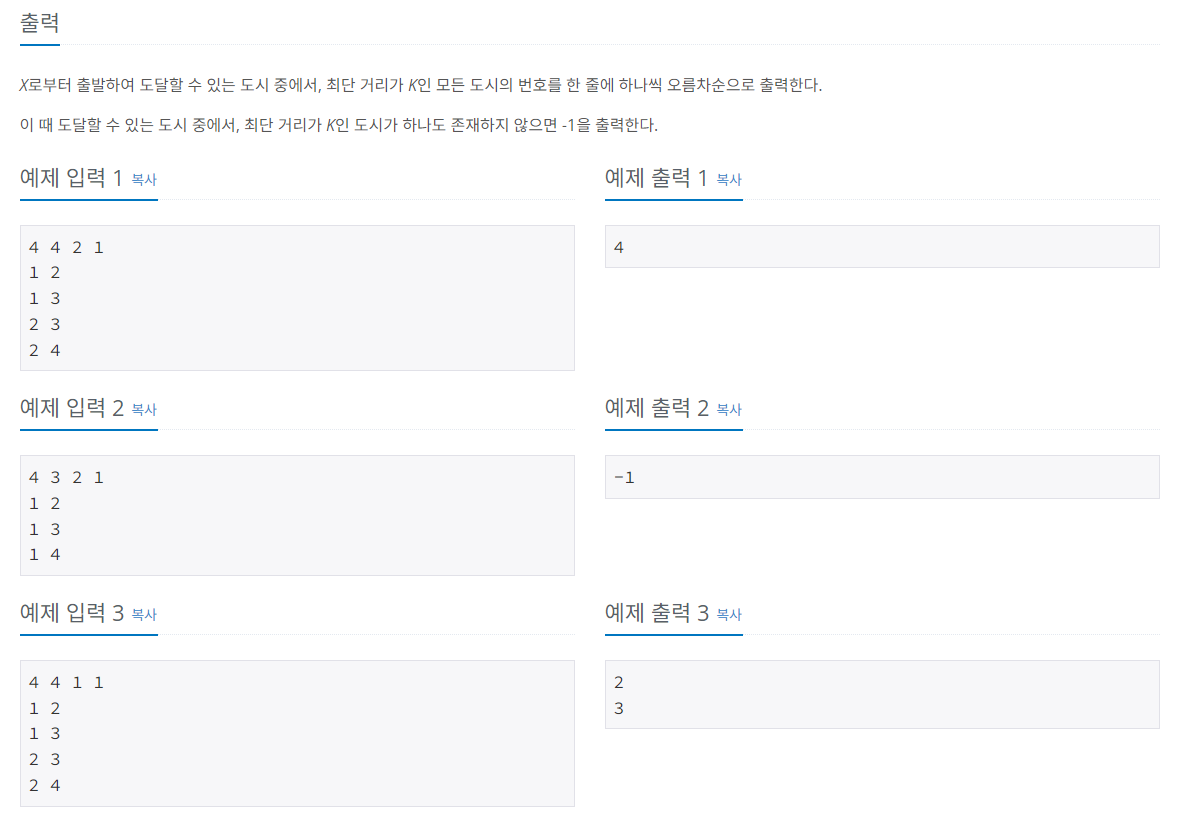
내 문제 접근 방법

1, 그래프 구성

• 주어진 도시와 도로를 단방향 인접 리스트 loads로 나타내어 그래프를 구성했습니다. 각 도시는 정점, 도로는 간선으로 표현되며, BFS를 통해 각 도시로의 최단 거리를 탐색할 수 있도록 구현했습니다.

2, BFS를 이용한 최단 거리 탐색

• 최단 거리 문제에서 BFS를 활용하면, 시작점으로부터 각 도시로의 최단 거리를 계산할 수 있습니다.
• visited 배열을 통해 각 도시의 방문 여부와 시작점에서의 최단 거리를 기록하였습니다. visited[X] = 0으로 시작점을 초기화하고 BFS를 수행하여 도달할 때마다 거리를 1씩 증가시켰습니다.

3, 최단 거리 조건을 만족하는 도시 출력

• BFS 탐색 후 visited 배열을 확인하여 거리가 정확히 K인 도시들을 출력했습니다.
• 거리가 K인 도시가 없다면 -1을 출력하여 예외 상황을 처리했습니다.

내 코드

// ConsoleApplication1.cpp : 이 파일에는 'main' 함수가 포함됩니다. 거기서 프로그램 실행이 시작되고 종료됩니다.
//

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int N, M, K, X;
vector<vector<int>> loads;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    std::cin >> N >> M >> K >> X;

    loads = vector<vector<int>>(N + 1);
    for(int i = 0; i < M; i++)
    {
        int y, x = 0;
        std::cin >> y >> x;
        loads[y].push_back(x);
    }

    vector<int> visited = vector<int>(N + 1,-1);

    queue<int> q;
    q.push(X);
    visited[X] = 0;
    while (!q.empty())
    {
        int current = q.front();
        q.pop();

        for(auto next : loads[current])
        {
            if (visited[next] != -1) continue;
            visited[next] = visited[current] + 1;
            q.push(next);
        }
    }

    bool founded = false;

    for(int i = 0; i < visited.size(); i++)
    {
        //std::cout << i << " : " << visited[i] << '\n';
	    if(visited[i] == K)
	    {
            std::cout << i << '\n';
            founded = true;
	    }
    }
    if(!founded)
        std::cout << -1 << '\n';
	return 0;
}

 

배운 점

1, BFS의 최단 거리 탐색 특성 : BFS는 각 단계에서 모든 인접 정점을 방문하므로, 출발점에서부터 일정 거리를 유지하며 탐색할 수 있습니다. 이 점을 활용해 최단 거리를 빠르게 계산할 수 있음을 다시 확인했습니다.

 

2, 예외 상황 처리 : 문제에서 주어진 조건을 만족하지 못하는 경우 예외 처리가 중요합니다. visited 배열에 거리 기록을 남기지 않거나 초기값 -1을 유지하는 방법으로 해결할 수 있음을 배웠습니다.

 

3, 단방향 그래프의 구현 : 단방향 그래프를 통해 양방향 그래프와 다른 특성을 다루는 연습이 되었고, 입력이 단방향일 때는 loads[a].push_back(b)만 추가하여 구현할 수 있다는 점을 다시 익혔습니다.

결론

이번 문제를 통해 BFS의 활용성과 최단 거리 탐색의 중요성을 체감할 수 있었습니다. 단방향 그래프와 BFS를 적절히 사용해 최단 거리 문제를 해결하는 연습이 되었으며, 앞으로도 다양한 그래프 문제에 적용할 수 있을 것이라 생각됩니다.