-
[DirectX11] Triangle의 Point Test,Interaction,Raycast2024년 03월 14일
- 유니얼
-
작성자
-
2024.03.14.:14
728x90DirectX 11로 게임 엔진 아키텍처 만들기
3D 그래픽스와 게임 개발에서 삼각형은 가장 기본적인 구성 단위 중 하나입니다. 복잡한 메시(mesh)와 모델들은 수천, 수백만 개의 삼각형으로 이루어져 있으며, 이러한 삼각형들과의 상호작용은 게임 엔진과 물리 엔진에서 중요한 역할을 합니다. 이 글에서는 삼각형과 점의 관계, 삼각형과 레이(ray)의 교차 검사 방법 등을 포함하여 삼각형과 관련된 다양한 계산 방법들을 탐구합니다.
참고강의 링크:
[게임 프로그래머 도약반] DirectX11 입문 강의 - 인프런
게임 프로그래머 공부에 있어서 필수적인 DirectX 11 지식을 초보자들의 눈높이에 맞춰 설명하는 강의입니다., [사진][사진] [사진] 게임 개발자는 Unreal, Unity만 사용할 줄 알면 되는 거 아닌가요? 엔
www.inflearn.com
점이 삼각형 내부에 있는지 검사하기
점이 주어진 삼각형 내부에 있는지 확인하는 방법 중 하나는 삼각형을 구성하는 벡터들을 사용하여 교차 벡터(cross vector)를 계산하고, 이들의 내적(dot product)을 검사하는 것입니다. 이 방법은 간단하면서도 효율적으로 점의 위치를 삼각형에 대해 판단할 수 있게 해줍니다.

// 점이 삼각형 내부에 있는지 판단하는 함수 bool MathUtils::PointInTriangle(const Point3D& p, const Triangle3D& t) { Vec3 a = t.a - p; // 점 p에서 삼각형의 꼭짓점 a로의 벡터 Vec3 b = t.b - p; // 점 p에서 삼각형의 꼭짓점 b로의 벡터 Vec3 c = t.c - p; // 점 p에서 삼각형의 꼭짓점 c로의 벡터 // 삼각형의 각 변에 대해 점 p를 포함하는 평면의 법선 벡터 계산 Vec3 normPBC = b.Cross(c); // PBC의 법선 벡터 (u) Vec3 normPCA = c.Cross(a); // PCA의 법선 벡터 (v) Vec3 normPAB = a.Cross(b); // PAB의 법선 벡터 (w) // 법선 벡터들의 방향이 모두 같은지 확인하여 점이 삼각형 내부에 있는지 판단 if (normPBC.Dot(normPCA) < 0.0f) return false; // PBC와 PCA 법선 벡터가 서로 반대 방향이면 점은 삼각형 내부에 없음 else if (normPBC.Dot(normPAB) < 0.0f) return false; // PBC와 PAB 법선 벡터가 서로 반대 방향이면 점은 삼각형 내부에 없음 return true; // 그 외의 경우 점은 삼각형 내부에 있음 }삼각형으로부터 평면 생성하기
삼각형을 구성하는 점들로부터 평면의 방정식을 생성할 수 있습니다. 이는 삼각형의 두 벡터를 교차하여 법선 벡터(normal vector)를 얻고, 이를 통해 평면의 방정식을 도출하는 과정을 포함합니다. 평면의 방정식은 다양한 충돌 검사와 물리 계산에 사용될 수 있습니다.
// 삼각형으로부터 평면을 생성하는 함수 Plane3D MathUtils::FromTriangle(const Triangle3D& t) { Plane3D result; // 삼각형의 두 변의 벡터를 외적하여 평면의 법선 벡터를 계산 result.normal = (t.b - t.a).Cross(t.c - t.a); result.normal.Normalize(); // 법선 벡터를 정규화 // 평면의 거리 계산 (법선 벡터와 삼각형의 한 꼭짓점의 내적으로 계산) result.distance = result.normal.Dot(t.a); return result; }삼각형과 레이의 교차 검사
삼각형과 레이의 교차 검사는 레이 트레이싱(ray tracing), 충돌 검사, 가시성 판단 등 다양한 분야에서 중요합니다. 평면과 레이의 교차 점을 찾고, 이 점이 실제로 삼각형 내부에 있는지를 판단하여 교차 여부를 결정합니다.
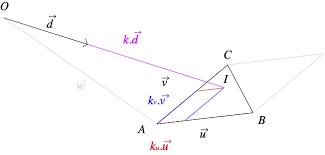
// 미구현된 함수, 삼각형 내의 점에 대한 바리센트릭 좌표를 계산 Vec3 MathUtils::Barycentric(const Point3D& p, const Triangle3D& t) { // 이 함수는 여기에서 구현되지 않았습니다. return Vec3(); } // 레이와 삼각형의 충돌 검사 bool MathUtils::Raycast(const Triangle3D& triangle, const Ray3D& ray, OUT float& distance) { Plane3D plane = FromTriangle(triangle); // 삼각형으로부터 평면 생성 float t = 0; // 레이와 평면의 충돌 검사 if (!Raycast(plane, ray, OUT t)) return false; // 충돌하지 않으면 false 반환 // 충돌 지점 계산 Point3D result = ray.origin + ray.direction * t; // 충돌 지점에 대한 바리센트릭 좌표 계산 Vec3 barycentric = Barycentric(result, triangle); // 바리센트릭 좌표를 사용하여 충돌 지점이 삼각형 내부에 있는지 확인 if (barycentric.x >= 0.0f && barycentric.x <= 1.0f && barycentric.y >= 0.0f && barycentric.y <= 1.0f && barycentric.z >= 0.0f && barycentric.z <= 1.0f) { distance = t; // 충돌 거리 설정 return true; // 충돌 발생 } return false; // 충돌하지 않음 }벡터의 투영
벡터를 다른 벡터에 투영하는 연산은 광선 추적, 반사, 굴절 등의 계산에서 유용하게 사용됩니다. 특정 벡터를 다른 벡터에 정사영(projection)하면, 두 벡터 간의 상대적인 위치와 방향을 파악할 수 있습니다.
// 벡터 a를 벡터 b에 투영하는 함수 Vec3 MathUtils::ProjectVecOnVec(Vec3 a, Vec3 b) { b.Normalize(); // 벡터 b를 정규화 float dist = a.Dot(b); // 벡터 a와 정규화된 벡터 b의 내적 계산 return b * dist; // 투영된 벡터 반환 }결론
이러한 기본적인 수학적 개념과 계산 방법들은 3D 그래픽스 프로그래밍과 게임 엔진 개발의 기초를 이룹니다. 복잡한 3D 환경을 정확하게 모델링하고, 가상 세계 내의 객체들 사이의 상호작용을 구현하는 데 있어서, 이러한 기법들은 필수적인 도구입니다. 개발자들은 이러한 수학적 기반 위에 구축하여, 사용자에게 현실감 넘치는 가상 환경과 경험을 제공할 수 있습니다.
반응형다음글이전글이전 글이 없습니다.댓글