[프로그래머스] 하노이의 탑(C++)
하노이 탑(Tower of Hanoi) 문제는 고전적인 재귀 알고리즘 문제로, 재귀적인 사고를 키우기에 좋은 문제 중 하나입니다. 이 문제를 풀기 위한 알고리즘과 코드를 살펴보겠습니다.
문제링크:
https://school.programmers.co.kr/learn/courses/30/lessons/12946
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

문제 개요
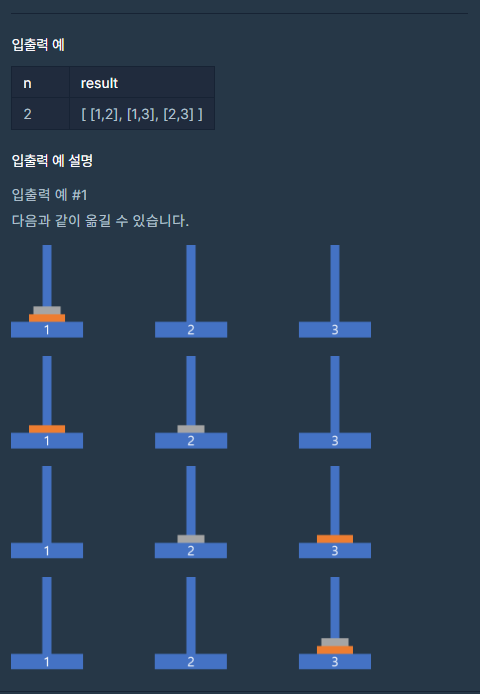
하노이 탑 문제는 세 개의 기둥과 이 기둥에 꽂을 수 있는 원판들로 구성되어 있습니다. 원판들은 크기가 다양하며, 처음에는 한 기둥에 작은 원판이 위에 오도록 쌓여 있습니다. 목표는 다음 두 가지 조건을 만족하면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것입니다.
- 한 번에 하나의 원판만 옮길 수 있습니다.
- 큰 원판이 작은 원판 위에 있어서는 안됩니다.
하노이 탑 문제의 세 개의 기둥을 왼쪽(L), 중간(M), 오른쪽(R)으로 표현하고, 시작 기둥에 있는 원판을 목표 기둥으로 최소한의 움직임으로 옮기는 것이 목표입니다.
알고리즘 설명
하노이 탑 문제를 해결하기 위한 알고리즘은 재귀적인 방법을 사용합니다. 기본 아이디어는 다음과 같습니다.
- 먼저, n-1개의 원판을 중간(M) 기둥으로 옮깁니다.
- 시작(L) 기둥에 남아 있는 가장 큰 원판을 목표(R) 기둥으로 옮깁니다.
- 중간(M) 기둥에 있는 n-1개의 원판을 목표(R) 기둥으로 옮깁니다.
이렇게 하면 n개의 원판을 최소한의 움직임으로 목표 기둥으로 옮길 수 있습니다.
문제 접근방법
1, 우선, 하노이 탑 문제의 목표는 원반을 1번 기둥에서 3번 기둥으로 최소 횟수로 옮기는 것입니다. 여기서 2번 기둥은 보조 기둥으로 사용됩니다.
2, 이 문제를 해결하기 위해서는 재귀 함수를 사용할 것입니다. 이 재귀 함수는 다음과 같이 정의할 수 있습니다.
Hanoi(n, from, to, aux)- n: 옮겨야 할 원반의 개수
- from: 출발 기둥 (1, 2, 3 중 하나)
- to: 목표 기둥 (1, 2, 3 중 하나)
- aux: 보조 기둥 (1, 2, 3 중 하나)
3, 재귀 함수의 동작 과정은 다음과 같습니다.
- 만약 n이 1이라면, 가장 작은 원반을 from 기둥에서 to 기둥으로 옮깁니다. 이것이 재귀 함수의 종료 조건입니다.
- 그렇지 않으면 다음 단계를 수행합니다.
a: n-1개의 원반을 from 기둥에서 aux 기둥으로 옮깁니다. 이때, to 기둥을 보조 기둥으로 사용합니다. 이 작업은 Hanoi(n-1, from, aux, to)를 호출하여 처리합니다.
b: 가장 큰 원반을 from 기둥에서 to 기둥으로 옮깁니다.
c: n-1개의 원반을 aux 기둥에서 to 기둥으로 옮깁니다. 이때, from 기둥을 보조 기둥으로 사용합니다. 이 작업은 Hanoi(n-1, aux, to, from)를 호출하여 처리합니다.
4, 이렇게 재귀 함수를 호출하면서 원반을 옮기는 과정을 반복하면, 모든 원반을 1번 기둥에서 3번 기둥으로 최소 횟수로 옮길 수 있습니다.
5, 각 단계마다 옮긴 원반의 출발 기둥과 목표 기둥을 기록하면, 최종적으로 모든 이동 경로를 구할 수 있습니다.
코드 구현
문제를 해결하기 위한 코드는 다음과 같습니다. C++을 사용하여 작성되었으며, 주석을 통해 코드의 각 부분을 설명하였습니다.
#include <string>
#include <vector>
#include <bits/stdc++.h> // 필요한 헤더 파일 포함
using namespace std;
// 탑을 위한 열거형 정의
enum Top {
A = 1,
B = 2,
C = 3,
};
vector<vector<int>> ret; // 이동 순서를 저장할 글로벌 변수
// 하노이 탑 문제를 해결하기 위한 재귀 함수
void Hinoi(int n, Top from, Top mid, Top to) {
vector<int> r;
if (n == 1) { // 기본 경우: 이동할 디스크가 하나만 있는 경우
r.push_back((int)from);
r.push_back((int)to);
ret.push_back(r); // 이동 기록
return;
}
// 'from'에서 'mid'를 거쳐 'to'로 n-1 개의 디스크를 이동
Hinoi(n - 1, from, to, mid);
r.push_back((int)from);
r.push_back((int)to);
ret.push_back(r); // 현재 디스크 이동 기록
Hinoi(n - 1, mid, from, to); // 나머지 디스크를 최종 목적지로 이동
}
// 하노이 탑 문제의 솔루션을 제공하는 함수
vector<vector<int>> solution(int n) {
Hinoi(n, A, B, C); // 하노이 함수 호출
return ret; // 이동 순서 반환
}결과 설명
위 코드는 하노이 탑 문제를 해결하기 위한 C++ 코드입니다. Hanoi 함수를 호출하여 원판을 옮기는 과정을 계산하고, 결과는 ret 벡터에 저장됩니다. 최종적으로 움직임의 수와 각 움직임의 내용이 출력됩니다.